In the field of wireless communications, the multiple-input, multiple output (MIMO) channel is experiencing increased interest due to the drammatic increases in capacity that result from adding multiple transmit and receive antennas to wireless systems. Early work in the area centered on channels with flat fading characteristics. Here, it was found that channel capacity increases linearly with the number of antennas used [1]. However, the simple transmit and receiver architectures that result from the assumption of flat fading are not easily reproduced when it is relaxed. Thus, one topic of recent work has been appropriate receiver (and in some cases, transmitter) architectures for channels with intersymbol interference (ISI, e.g., frequency-selective fading).
The purpose of this project is to compare the performance of three MIMO system architectures in the presence of ISI. Two architectures are implemented in the receiver only. First, the optimal finite-length MIMO minimum-mean-square-error decision feedback equalizer (MMSE DFE) is computed (as reported in [2]). In this case, the equalization occurs using the matrix analogue of a standard single-input, single-output (SISO) DFE. Second, a multi-stage equalization structure is implemented (as in [3], where the authors expand on a multi-stage MIMO reciever architecture presented in [4]).
Recall that in [1], it is shown that the optimum structure for MIMO transmission in a flat-fading environment uses a channel decomposition that involves signal processing both at the receiver and transmitter. Thus, one would expect that the optimal system structure in an ISI environment would also involve transmitter-side processing, which neither of the two previous systems involve. In [5], an "discrete matrix-multitone" architecture is presented in which the channel is decomposed in a way analagous to the SISO DMT. This third architecture's performance is compared to the previous two receiver-only implementations. The performance metric used in all three cases is the simulated BER as a function of channel SNR. Several multi-input, multi-output channels are generated using random multipath components, with a four transmit antenna, four receieve antenna architecture (as in [5], example 1).
In the field of wireless communications, the multiple-input, multiple output (MIMO) channel is experiencing increased interest due to the drammatic increases in capacity that result from adding multiple transmit and receive antennas to wireless systems. Early work in the area centered on channels with flat fading characteristics. Here, it was found that channel capacity increases linearly with the number of antennas used [1]. However, the simple transmit and receiver architectures that result from the assumption of flat fading are not easily reproduced when it is relaxed. Thus, one topic of recent work has been appropriate receiver (and in some cases, transmitter) architectures for channels with intersymbol interference (ISI, e.g., frequency-selective fading).
The author compares the performance of the optimal finite-length MIMO minimum-mean-square-error decision feedback equalizer (MMSE DFE) with channel transmission using a Discrete Matrix Multitone (DMMT) system in the presence of small amounts of ISI.
In [1], it is shown that the optimum structure for MIMO transmission in a flat-fading environment uses a channel decomposition that involves signal processing both at the receiver and transmitter.� In the more general situation with frequency-selective fading, the optimum architecture is less obvious.� Current system implementations in which multi-user detection (a form of a MIMO system) is performed typically involve CDMA, which can eliminate ISI by spreading it in frequency, or else lessen its impact drastically.� In these cases, the typical architecture utilized is a decision-feedback equalizer.� However, alternatives have been discussed, the most promising of which seems to be the MIMO analogue of discrete multitone, or discrete matrix multitone.� Here, the ISI is essentially eliminated through spatial frequency division.
In [2], fast methods are presented for computing the optimal FIR filter coefficients for a MIMO MMSE-DFE.� Three architectures are discussed: the general multi-channel analogue of the SISO DFE; a situation where channels are decoded sequentially each symbol period, and thus current decisions are available for previously decoded channels (similar in spirit to the architecture in [3]), and the situation in which all channels� current decisions are simultaneously known (how this would occur in practice is unclear).� Three things must be optimized in the system for a given FIR feed-forward filter length: the filter delay, the feedback filter coefficients, and the feed-forward filter coefficients.� If one assumes perfect decisions, having error uncorrelated with channel output (orthagonality, or E[ekyk*] = 0) implies that the feed-forward coefficients can be found from the formula:
Wopt* = Bopt* Rxy Ryy-1
One of the advantages of the DFE architecture is that it is implemented only on the receiver.� Despite this, however, it is still necessary to estimate the impulse responses of each of the MR*MT channels.� In situations in which the channel is changing rapidly, this may be a substantial impediment to system implementation.
As previously mentioned, the MIMO DFE architecture is implemented only on the receiver.� Since it�s clear that an optimal system design will involve some transmitter-side processing, the question to answer is what the optimal system (transmitter and receiver) design is.� In [5], the MIMO analog of DMT is presented.� This system involves a small time overhead (from pre-transmitting the last few symbols in a block before the block), but allows for an elegant solution.� In this situation, the inverse fast fourier transform, and the fast fourier transform are basis vectors, and thus can diagonalize, the channel matrices. Mathematically, if H is composed of Hnm, the sub-matrix representing the circular transmission of a block of N data points from transmitter n to receiver m, then:
F H F* = [Enm]
where Enm represents the block diagonal matrices of eigenvalues and F is a block diagonal DFT matrix. Thus, permuting the result with permutation matrices PT and PR results in a block diagonal matrix, G.
PR F H F* PT = G
Each of the MRxMT blocks can then be diagonalized using the singular value decomposition, and thus the diagonalization of the channel is completed.� If :
G = U S V*
then,
Y = U* PR F H F* PT V X = S X
After channel estimation, the system implementation only really requires the calculation of the svd of the channel coefficient matrices, which will be small (MRxMT).� Thus, the implementation of DMMT may actually be more feasible, in a changing channel environment, than the MIMO DFE, a somewhat surprising result.
2x2 channel impulse responses were generated for 40 different channels. Each impulse response was assumed to be three taps, with normally distributed real coefficients.� After the coefficients were calculated, each impulse response was normalized to unit energy.� This channel model was used because of its simplicity (and ease of calculation).� Future work would involve more realistic models.� Transmission was assumed to be BPSK.� Because the channels are unit energy, a measure of receiver SNR is simply the inverse of the noise power.
For each channel, the pseudo-optimum (feed-back fixed to one tap, with knowledge only of past decisions) MIMO DFE coefficients were calculated for a 6 tap feed-forward filter.� The channel diagonalization for a DMMT implementation with a block size of 16 symbols was also calculated.� Note that optimally, the input signals to each DMMT subchannel would be adapted in power and/or bits/symbol given the knowledge of the diagonal channel transmission functions.� However, this was not implemented due to time constraints.
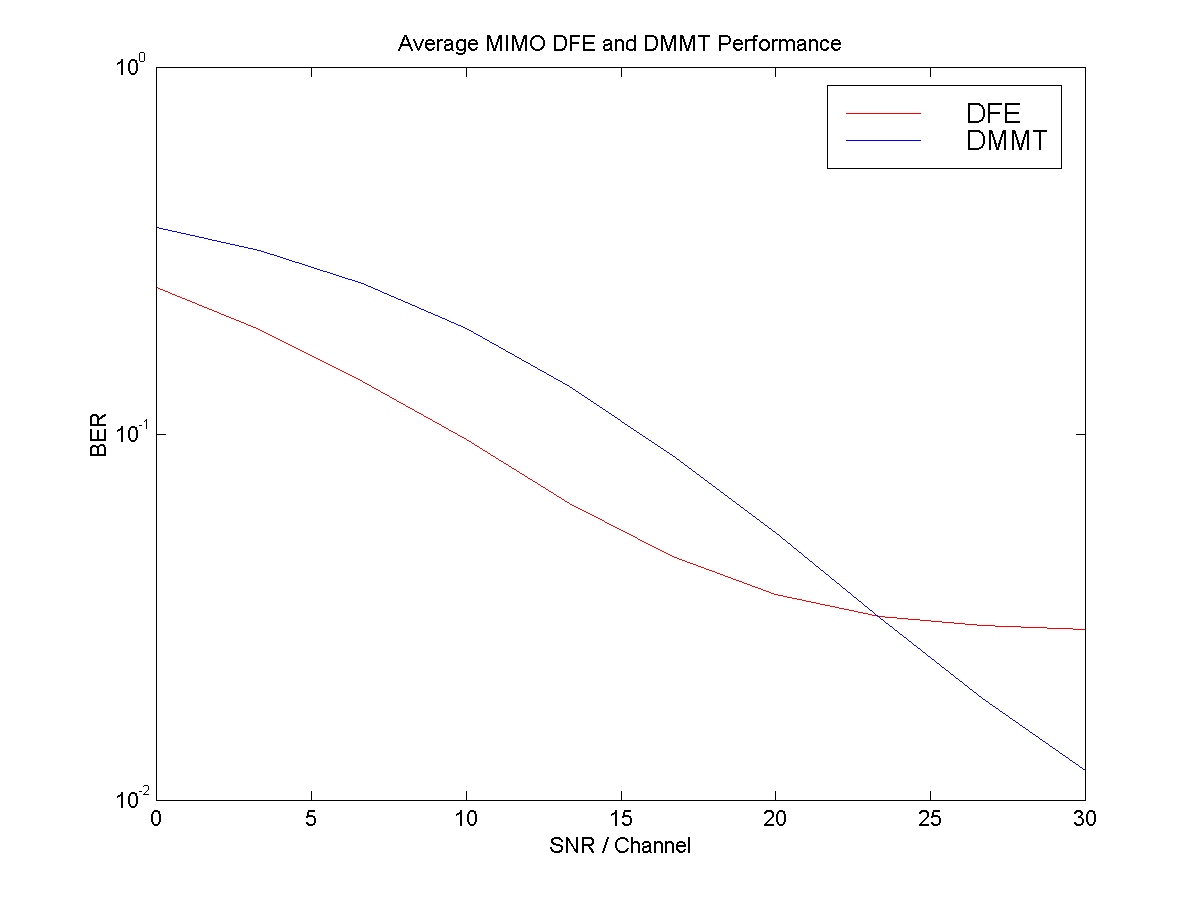
20,000 random bits were generated, and the number of bit errors was calculated at the output of the DFE and DMMT.
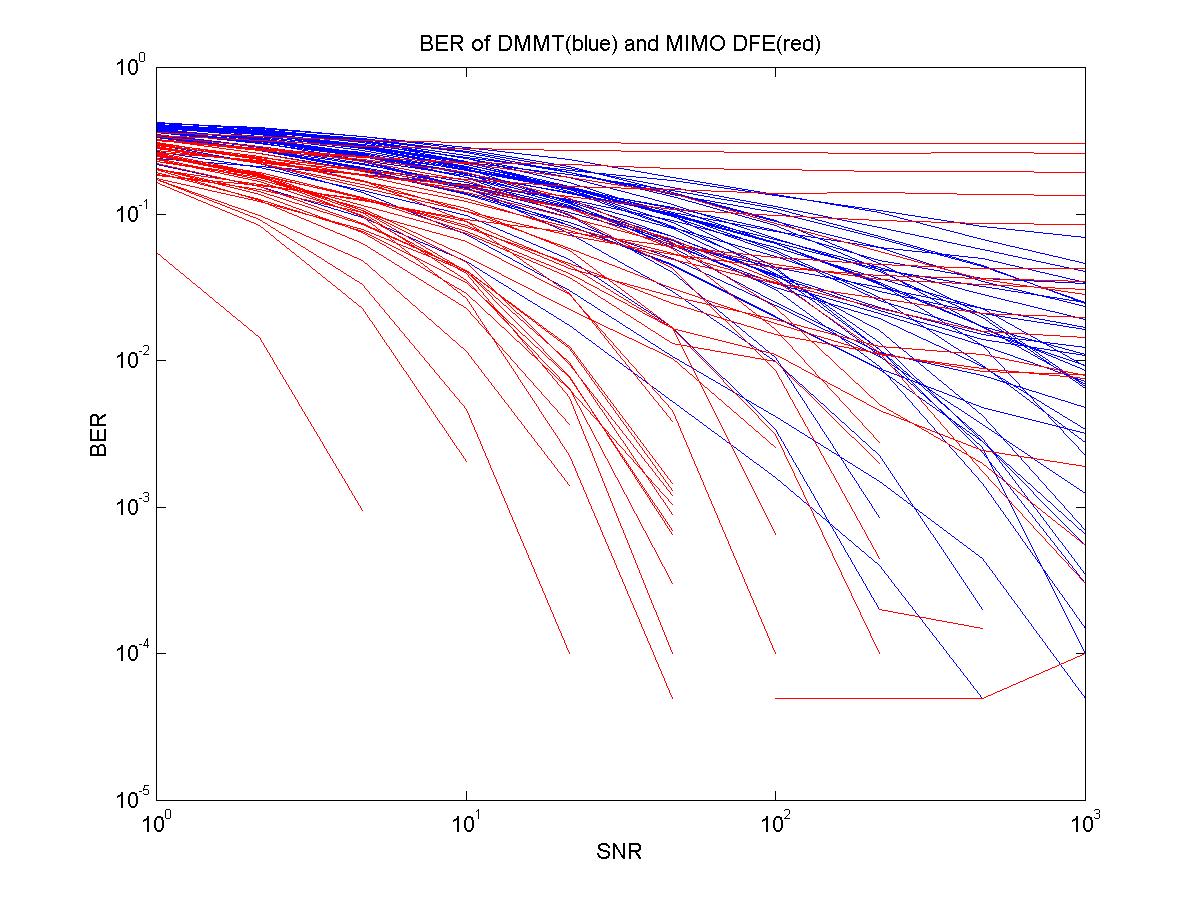
The results are shown in the figures below.� Notice that the DMMT almost always performs slightly more poorly than the DFE.� (This is in addition to the data rate penalty that is incurred because of the block prefixes.)� However, in certain (perhaps pathological) cases, the DFE performs very poorly, whereas the DMMT is consistent.� This suggests the classic problem with decision-feedback, error propagation, is not only present in MIMO situations, but even worsens. The average BER curve for the DFE displays the classic shape of an error floor. While it's nice to think that this is a result of error propagation, this is not clear. The limiting BER may also be (in some way) a result of the channel model.
Implementation
Notes
The DMMT was implemented somewhat smoothly, without any large apparent errors.� Results are as expected, and channel decomposition computation time was not excessive (as might have been feared). The MIMO DFE implementation was much more difficult. Despite the fact that the results presented in [2] for a 2x2 channel were easily repeated, when the system was expanded to optimally create more than one tap in the feedback filters, the performance degraded tremendously. This suggests an implementation flaw. However, the implementation seemed to be working for the obvious cases (e.g., diagonal channels), so it is unclear what, if anything was wrong. One possibility might be that because the optimal feedback filter settings are calculated assuming perfect decisions, they do not take the error propagation that will increase as the number of feedback taps increases. To ensure that implementation was not at issue, further work on this front would be a good idea.
A sample of the matlab code can be found here. This particular sample does 20 channels with 10 different noise powers per channel. A typical single-channel, single-noise-power simulation with 2e4 data points takes about 30 seconds on the fast sparcstations.
The results of this study somewhat surprisingly suggest that DMMT, a system in which there are optimal transmitter and receiver filter operations does not perform dramatically better than the MIMO DFE, a receiver-only system. However, as previously mentioned, a critical portion of DMMT system implementation, power and/or bit rate adaptation, was not implemented, and might have improved performance. Furthermore, because the bit error rates tested where somewhat high (on the order of 1 in 1000), the problem of error propagation, though noticeable, was not highlighted as it might have been if the system was tested at very low bit error rates (in which one error cascades into many). Finally, the channel that was used for comparison is not realistic (though it is unlikely that this would have affected the results).Future work would have to address DMMT adaptation, and better channel models, and perhaps even channel and filter coefficient estimation times.
A system level analysis suggests that perhaps, compared to the MIMO DFE, the DMMT provides equivalent performance with (assuming simple FFT implementation) only slightly more implementation complexity, as well as allowing for faster filter estimation (a simple svd) in changing channel situations. However, when considered from a multiple user perspective, the MIMO DFE has the advantage that it can be used in situations in which multiple users with single antennas transmit to a base station with multiple antennas, whereas, because it requires permutation of the channel inputs, the DMMT will not work in this situation. Thus, for high speed wireless links in which both transmitter and receiver have multiple antennas, the DMMT is probably an optimal solution. However, for intra-cell frequency reuse, clearly the DMMT (as presented) will not work, and thus a MIMO DFE is required. This suggests an avenue of further effort: perhaps the ISI rejection of the DMMT can somehow be combined (in perhaps a slightly less optimal way), with a multiple antenna receiver.
The area of transmitter and receiver architectures for wideband MIMO channels is clearly important, and also appears to hold promise for future research.